Measures of Dispersion – Range, Variance, Standard Deviation, Interquartile Range 📐
🎯 Learning Objectives
By the end of this lesson, you will be able to:
✔ Define and calculate Range, Variance, Standard Deviation (SD), and Interquartile Range (IQR)
✔ Understand their interpretation in medical data
✔ Know why dispersion is important alongside central tendency
1️⃣ Introduction
Knowing the average (mean, median) is not enough. We also need to know how spread out the data is.
This is called dispersion. Two datasets can have the same mean but very different spreads, which can change interpretation in clinical research.
Common measures of dispersion:
✅ Range
✅ Variance
✅ Standard Deviation (SD)
✅ Interquartile Range (IQR)
2️⃣ Range
Definition:
- The difference between the largest and smallest value in the dataset.
✔ Formula:
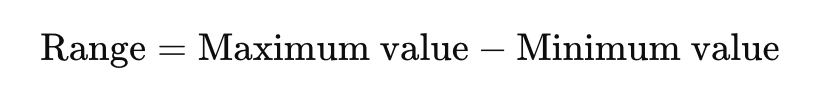
✔ Example:
BP readings: 110, 120, 130, 140, 150
Range = 150 – 110 = 40 mmHg
✔ Key Features:
- Simple but affected by outliers
- Gives only the extreme spread, not the distribution
3️⃣ Variance
Definition:
- The average of the squared differences from the mean.
✔ Formula:
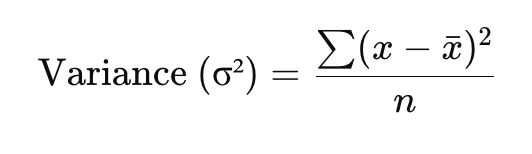
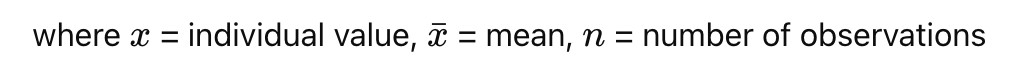
✔ Example:
If mean = 100, values = 90, 100, 110
Differences = -10, 0, +10 → Squares = 100, 0, 100
Variance = (100 + 0 + 100)/3 = 66.67
✔ Key Features:
- Always positive
- Units are squared (not very interpretable clinically)
4️⃣ Standard Deviation (SD)
Definition:
- The square root of the variance.
- Indicates how much values typically deviate from the mean.
✔ Formula:
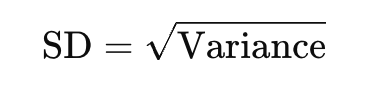
✔ Example:
From above, Variance = 66.67 → SD = √66.67 ≈ 8.16
✔ Key Features:
- Most widely used measure of dispersion
- Used in confidence intervals, normal distribution
✔ Clinical Interpretation:
- In a normal distribution:
- 68% values lie within ±1 SD
- 95% values within ±2 SD
- 99.7% values within ±3 SD
5️⃣ Interquartile Range (IQR)
Definition:
- The range between the 25th percentile (Q1) and 75th percentile (Q3).
- It captures the middle 50% of the data, removing extreme values.
✔ Formula:
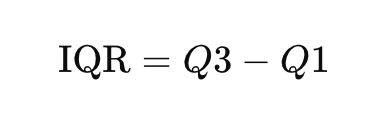
✔ Example:
Data: 5, 7, 8, 10, 12, 13, 15
Q1 = 7, Q3 = 13 → IQR = 13 – 7 = 6
✔ Key Features:
- Not affected by outliers
- Best for skewed data
6️⃣ Comparison Table
| Measure | Formula | Affected by Outliers? | Use Case |
|---|---|---|---|
| Range | Max – Min | ✅ Yes | Quick estimate of spread |
| Variance | Average of squared differences | ✅ Yes | Basis for SD |
| Standard Deviation | √Variance | ✅ Yes | Most common in research |
| IQR | Q3 – Q1 | ❌ No | Best for skewed data |
7️⃣ Clinical Relevance
- Range: Quick spread in BP or lab values
- SD: Used in reporting clinical trial results
- IQR: Used in non-parametric statistics, skewed hospital stay data
8️⃣ Quick Check: Test Your Understanding ✅
Q1: Which measure is most affected by extreme values?
a) Range
b) SD
c) IQR
👉 Answer: a) Range
Q2: If Q1 = 20 and Q3 = 30, what is IQR?
👉 Answer: 10
Q3: Which measure is best for skewed data?
👉 Answer: IQR
✨ Key Takeaways
- Range: Simple but outlier-sensitive
- Variance: Basis for SD, not easily interpretable
- Standard Deviation: Most widely used, key for normal distribution
- IQR: Best for skewed data, ignores extremes